向量的线性相关、矩阵的秩总结
此贴搬运自本人曾经的博客,请读者悉知。
一些杂谈(可以不看)
这次尝试使用了MD记笔记。我这人真的挺奇怪,对着电脑记笔记比对着纸笔更专注。。。希望期末线代高数大物不会抛弃我。。。
以下是正文:
本文综合了网络各处的大佬的想法,综合总结成了笔记,仅作个人学习用。如我的行为如果有冒犯到您,请联系我,我将立即修改或删除。
前置概念
向量组和向量组的线性表示
如果向量组 $ B:\beta_1,\beta_2…\beta_q $ 中的每个向量都可由向量组 $ A:\alpha_1,\alpha_2…\alpha_n $ 线性表示,则称向量组B可由向量组A线性表示。(也称为两个向量组等价)
假设 $ B $ 由 $ A $ 表示:
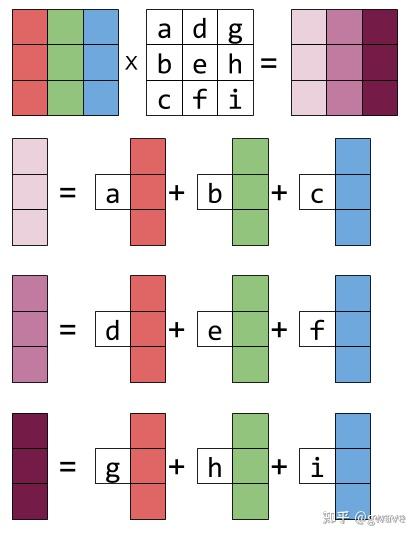
\[\left\{\begin{matrix} \beta = c_{11}\alpha_1+c_{21}\alpha_2+\cdots+c_{p1}\alpha_p\\ \beta = c_{12}\alpha_1+c_{22}\alpha_2+\cdots+c_{p2}\alpha_p\\ \cdots \\ \beta = c_{13}\alpha_1+c_{23}\alpha_2+\cdots+c_{p3}\alpha_p \end{matrix}\right.\]观察可知:一个向量组表示另一向量组就是矩阵乘法的关系。因此我们改写为矩阵形式:
\[\begin{bmatrix}\beta_1 ,\beta_2, \cdots ,\beta_3 \end{bmatrix}= \begin{bmatrix}\alpha_1 ,\alpha_2, \cdots ,\alpha_3 \end{bmatrix} \begin{bmatrix} c_{11} & c_{12} & \cdots &c_{1q} \\ c_{21} & c_{22} & \cdots &c_{2q} \\ \vdots & \vdots & &\vdots \\ c_{p1} & c_{p2} & \cdots &c_{pq} \end{bmatrix}_{p\times q}\]即:$ B=A\times C $ 系数矩阵。
性质
若向量组 $ \alpha_1,\alpha_2,\cdots,\alpha_s $ 可被向量组 $ \beta_1,\beta_2,\cdots,\beta_t $ 线性表示,则: \(R(\alpha_1,\alpha_2,\cdots,\alpha_s)\le R(\beta_1,\beta_2,\cdots,\beta_t)\)
这里需要用到秩的概念,建议看完下面再来这里。
线性相关
定义
如果一组向量中至少有一个是多余的,没有对张成空间作出任何贡献,你有多个向量,并且可以移除其中一个而不减少张成的空间,称线性相关。
对于一个二维空间,只需要任意两个不共线的非零向量即可张成整个空间。此时称这两个向量线性无关;
假如此刻再次加入任意一个属于该空间的向量,这个新的向量对构成此空间没有任何作用(删掉它不影响空间的形成),则现在称这三个向量线性相关。此向量便是冗余的。
线性无关也可理解为:在张成的最大空间上,每个维度有且只有一个支撑向量的向量组。
另一种定义(百度百科、书本)
在向量空间V的一组向量 $a_1,a_2…a_m$ ,如果存在不全为零的数 $k_1, k_2,…,k_m$ ,使: \(k_1a_1+k_2a_2+...+k_ma_m=0\) 那么称向量组A是线性相关的。
这个概念不够直观,但是 可以用来计算、判断。
极大无关组(极大线性无关向量组)
记得前文提到的一组有冗余向量的向量组吗?在这一组向量组中取一部分的向量,让这一部分向量不仅线性无关,并且不能再加入更多向量继续保持线性无关,那么这一组向量就是原向量组的极大无关组。因此:向量组与它的极大无关组等价。
也就是说,当我们删除一个向量组的所有冗余向量后,剩下的就是原向量组的极大无关组。
极大无关组可能不唯一,但其包含的向量数一定唯一。
线性组合
$n$ 个向量 $\alpha$(的倍数)相加形成新的向量 $\beta$ :
\[\beta = \sum_{i=1}^{n}k_i\alpha_i\]则称向量 $\beta$ 是向量组 $\alpha_i$ 的一个线性组合,向量 $\beta$ 可由向量组 $\alpha_i$ 的线性表示。
理解线性相关和线性表示的关系
一组线性相关的向量组,其中必定有向量是其他向量的线性组合。
若最大空间的子空间拥有冗余向量(可以找到线性组合),则向量组线性相关。
正交向量组
正交:垂直; 两两正交的向量组被称为正交向量组; 若都为单位向量,则被称为规范正交向量组。
线性相关的简单性质
正交向量组线性无关;
含零向量的向量组线性相关;
向量组线性相关 $\Leftrightarrow$ 向量组中至少有一个向量是冗余的 $\Rightarrow$ $n+1$ 个 $n$维向量总是线性相关。个数大于维数必相关
不太直观的性质
如果向量组 $[a_1,a_2,a_3…a_n]$ 线性无关,向量组 $[a_1,a_2,a_3…a_n,b]$ 线性相关,那么: 向量 $b$ 可由向量组 $[a_1,a_2,a_3…a_n]$ 线性表示,且表达式的系数唯一确定。
证明?不想看书了,教材写得好差,有时间再补上吧。。。
线性无关向量组的加长向量组仍然线性无关。
但是什么是加长向量组?
假如二维向量$a(x,y)$增加了一个分量(维度),变成了$a(x,y,z)$,这个向量就加长了。假如向量组里的每一个向量都加长了,就形成了加长向量组。
可以想象平面内的两个向量同时向第三维增加一个分量的情况。两个向量虽然在三维空间里面形成了一个新的平面,但仍未升维,两个向量不可能凭空多出一个维度,也不会因为到了新的平面而平白无故共线。
狗嘴里吐不出象牙。
矩阵的秩
通俗理解
矩阵的秩,代表了某个方程组(向量组)的有效方程个数。
在对方程组(系数矩阵)进行化简(阶梯矩阵)之后,会发现有的矩阵表面看上去“满满当当”,实际上有好多没有起到作用的 $0$ 行!!
比如对于矩阵 $A$ :
\[\begin{bmatrix}1&1&2&3\\1&-1&4&1\\1&2&1&4\\1&1&2&3\end{bmatrix}\Rightarrow \begin{bmatrix}1&0&3&2\\0&1&-1&1\\0&0&0&0\\0&0&0&0\end{bmatrix}\]虽然是 $4$ 阶方阵,但化简之后非 $0$ 行只有 $2$ 行,因此其秩为 $2$ :
\[R(A)=2\]记得前面的极大无关向量组吗?它包含的向量个数就是这个向量组的秩。
相关概念
如果一个方阵的秩等于其行数,那么称这种矩阵为满秩矩阵,否则称为降秩矩阵。
因为一个可逆矩阵的行列式一定不为0,而矩阵的秩为非零子式的最高阶数,所以可逆矩阵一定是满秩矩阵。
假设一个秩不满的矩阵,对于它最大的满秩子方阵,我们称这个子方阵为最高阶非0子式。所以上面提到的矩阵$A$的最高阶非0子式为:
\[\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}\]从线性变换的角度来说,矩阵是对于整个空间的变换。而这个矩阵的秩代表了变换后的空间的维度。
因此,一个矩阵的逆矩阵表示了将扭曲后的空间变回原来样子的操作。
只有在同维度下,可逆才有意义。若空间被降维,信息会丢失,那么就不再能变回以前的空间了。(此处可想像3B1B视频里面二维空间被压缩到一维的动画)
我想再去复习一下3B1B的这个视频
列空间、行空间复习
这里复习此概念是为了更好地理解矩阵的秩的部分性质。
一般矩阵乘法计算方法:
\[\begin{bmatrix}1 &4 \\2 &5 \\3 &6\end{bmatrix} \begin{bmatrix}x_1 \\x_2 \end{bmatrix} =\begin{bmatrix} 1x_1+4x_2 \\ 2x_1+5x_2 \\ 3x_1+6x_2 \end{bmatrix}\]这种以行为主的内积运算适合电脑计算,但是不利于理解。
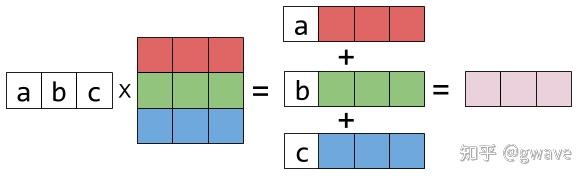
因此我们引入一个更高维度的视角——列向量: \(\begin{bmatrix} {\color{Orange} 1}&{\color{Purple} 4}\\{\color{Orange} 2}&{\color{Purple} 5}\\{\color{Orange} 3}&{\color{Purple} 6}\end{bmatrix} \begin{bmatrix}x_1 \\x_2 \end{bmatrix} =x_1\begin{bmatrix} {\color{Orange} 1}\\{\color{Orange} 2}\\{\color{Orange} 3}\end{bmatrix}+ x_2\begin{bmatrix} {\color{Purple} 4}\\{\color{Purple} 5}\\{\color{Purple} 6}\end{bmatrix}\)
来源知乎:矩阵乘法核心思想(1):列空间
而在 \(x_1 \begin{bmatrix} {\color{Orange} 1} \\ {\color{Orange} 2} \\ {\color{Orange} 3} \end{bmatrix}+x_2 \begin{bmatrix} {\color{Purple} 4} \\ {\color{Purple} 5} \\ {\color{Purple} 6} \end{bmatrix}\) 中,任意的 \(x_1,x_2\) 可以与这两个向量组合,张成一个空间。这个空间被称为这两个列向量所张成(Span)的列空间(Column Space)。
因此对应地,我们也有行空间 (Roll Space)存在:
来源知乎 矩阵乘法核心思想(2):行空间
矩阵的秩常用结论
- \[0\le R_{(A_{m\times n})}\le \min(m,n)\]
- \[R_{(A^T)}=R_{(A)}\]
- \[R\begin{bmatrix}A & 0 \\ 0 & B\end{bmatrix}=R\begin{bmatrix}0 & A \\ B & 0 \end{bmatrix} = R_{(A)}+R_{(B)}\]
- \[R\begin{bmatrix}A&0\\C&B\end{bmatrix}\ge R_{(A)}+R_{(B)}\]
矩阵乘以可逆矩阵,秩不变。如:\(R_{(B^{-1}AB)}=R_{(A)}\)
- \[R_{(A\pm B)}=R_{(A)}+R_{(B)}\]
- 重要性质!(西尔维斯特不等式) 若 $A$ 为 $m\times n$ 矩阵, $B$ 为 $n\times l$ 矩阵( $A,B$ 矩阵可以相乘),则:$R_{(A)}+R_{(B)}-n\le R_{(AB)}\le \min(R_{(A)},R_{(B)})$
证明:(证明过程较重要) 设置一个矩阵:\(\begin{bmatrix}A&0\\E_n&B\end{bmatrix}\) 可以知道经过初等变换,这个矩阵可以把左上角和右下角变为0: \(\begin{bmatrix}E_m&-A\\0&E_n\end{bmatrix}\begin{bmatrix}A&0\\E_n&B\end{bmatrix}\begin{bmatrix}E_n&-B\\0&E_l\end{bmatrix} =\begin{bmatrix}0&-AB\\E_n&0\end{bmatrix}\)
未完待续(也不会更了)